每逢碰到这个ANN的简称,小白菜总是想到Artificial Neural Network人工神经网络,不过这里要展开的ANN并不是Artificial Neural Network,而是已被小白菜之前写过很多次的Approximate Nearest Neighbor搜索。虽然读书的那会儿,这一块的工作专注得比较多,比如哈希,也整理过一个像模像样的工具包hashing-baseline-for-image-retrieval,以及包括KD树、PQ乘积量化等近似最近邻搜索,但这些东西放在今天小白菜的知识体系里来看,依然自以为还非常的散乱。所以借再次有专研的机会之际,再做一次整理,完善自己在索引这方面的知识体系。
在具体到不同类的索引方法分类前,小白菜以为,从宏观上对ANN有下面的认知显得很有必要:brute-force搜索的方式是在全空间进行搜索,为了加快查找的速度,几乎所有的ANN方法都是通过对全空间分割,将其分割成很多小的子空间,在搜索的时候,通过某种方式,快速锁定在某一(几)子空间,然后在该(几个)子空间里做遍历。可以看到,正是因为缩减了遍历的空间大小范围,从而使得ANN能够处理大规模数据的索引。
根据小白菜现有的对ANN的掌握,可以将ANN的方法分为三大类:基于树的方法、哈希方法、矢量量化方法。这三种方法里面,着重总结典型方法,其中由以哈希方法、矢量量化方法为主。
基于树的方法
几乎所有的ANN方法都是对全空间的划分,所以基于树的方法也不例外。基于树的方法采用树这种数据结构的方法来表达对全空间的划分,其中又以KD树最为经典。下面左图是KD树对全空间的划分过程,以及用树这种数据结构来表达的一个过程。
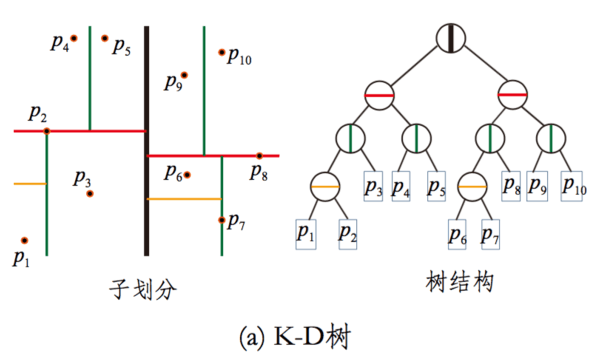
对KD树选择从哪一维度进行开始划分的标准,采用的是求每一个维度的方差,然后选择方差最大的那个维度开始划分。这里有一个比较有意思的问题是:为何要选择方差作为维度划分选取的标准?我们都知道,方差的大小可以反映数据的波动性。方差大表示数据波动性越大,选择方差最大的开始划分空间,可以使得所需的划分面数目最小,反映到树数据结构上,可以使得我们构建的KD树的树深度尽可能的小。为了更进一步加深对这一点的认识,可以以一个简单的示例图说明:
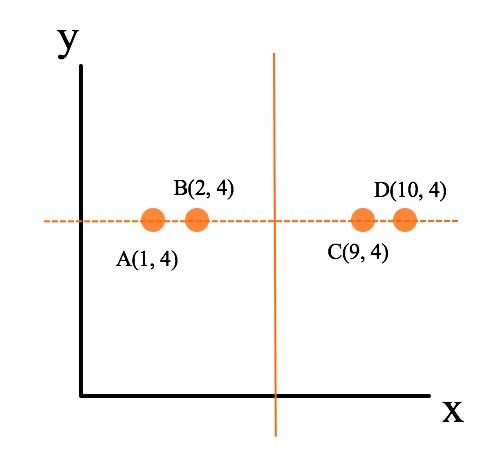
假设不以方差最大的x轴为划分面(x_var = 16.25),而是以y轴(y_var = 0.0)轴为划分面,如图中虚线所示,可以看到,该划分使得图中的四个点都落入在同一个子空间中,从而使得该划分成为一个无效的划分,体现在以树结构上,就是多了一层无用的树深度。而以x轴为初始划分则不同(图像实线所示),以x轴为初始划分可以得到数据能够比较均匀的散布在左右两个子空间中,从而使得整体的查找时间能够最短。注意,在实际的kd树划分的时候,并不是图中虚线所示,而是选取中值最近的点。上面示意图构建的具体kd树如下所示:
In [9]: kdtree.visualize(tree)
(9, 4)
(2, 4) (10, 4)
(1, 4)
一般而言,在空间维度比较低的时候,KD树是比较高效的,当空间维度较高时,可以采用下面的哈希方法或者矢量量化方法。
kd-trees are not suitable for efficiently finding the nearest neighbour in high dimensional spaces.
In very high dimensional spaces, the curse of dimensionality causes the algorithm to need to visit many more branches than in lower dimensional spaces. In particular, when the number of points is only slightly higher than the number of dimensions, the algorithm is only slightly better than a linear search of all of the points.
哈希方法
哈希,顾名思义,就是将连续的实值散列化为0、1的离散值。在散列化的过程中,对散列化函数(也就是哈希函数)有一定的要求。根据学习的策略,可以将哈希方法分为无监督、有监督和半监督三种类型。在评估某种哈希方法用于图像检索的检索精度时,可以使用knn得到的近邻作为ground truth,也可以使用样本自身的类别作为ground truth。所以在实际评估准确度的时候,根据ground truth的定义,这里面是有一点小的trick的。通常对于无监督的哈希图像检索方法,由于我们使用的都是未标记的数据样本,所以我们会很自然的采用knn得到的近邻作为ground truth,但是对于图像检索的这一任务时,在对哈希函数的构造过程中,通常会有“相似的样本经编码后距离尽可能的近,不相似的样本编码后则尽可能的远”这一基本要求,这里讲到的相似,指语义的相似,因而你会发现,编码的基本要求放在无监督哈希方法里,似乎与采用knn得到的近邻作为ground truth的评价方式有些南辕北辙。对无监督哈希方法的ground truth一点小的疑惑在小白菜读书的时候就心存这样的困惑,一直悬而未解。当然,在做无监督的图像哈希方法,采用样本自身的类别作为ground truth是毋庸置疑的。
小白菜读书那会儿,研究了很多的哈希图像检索方法(见hashing-baseline-for-image-retrieval),有时候总会给一些工程实践上的错觉(在今天看来是这样的),即新论文里的方法远远碾压经典的方法,那是不是在实际中这些方法就很work很好使。实践的经历告诉小白菜,还是经典的东西更靠谱,不是因为新的方法不好,而是新的事物需要经过时间的沉淀与优化。
所以,这里不会对近两年的哈希方法做铺陈,而是聊一聊工程中在要使用到哈希方法的场景下一般都会选用的局部敏感哈希(Local Sensitive Hashing, LSH)。
Local Sensitive Hashing
关于LSH的介绍,小白菜以为,Locality-Sensitive Hashing: a Primer这个讲解得极好,推荐一读。下面是小白菜结合自己的理解,提炼的一些在小白菜看来需要重点理解的知识(附上LSH划分空间示意图,在进行理解的时候可以参照改图)。
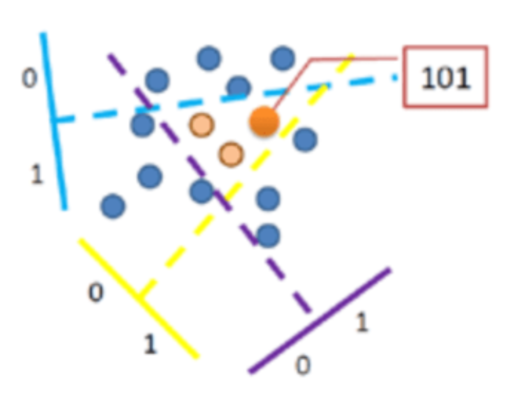
局部敏感是啥?
当一个函数(或者更准确的说,哈希函数家族)具有如下属性的时候,我们说该哈希函数是局部敏感的:相近的样本点对比相远的样本点对更容易发生碰撞。
用哈希为什么可以加速查找?
对于brute force搜索,需要遍历数据集中的所有点,而使用哈希,我们首先找到查询样本落入在哪个cell(即所谓的桶)中,如果空间的划分是在我们想要的相似性度量下进行分割的,则查询样本的最近邻将极有可能落在查询样本的cell中,如此我们只需要在当前的cell中遍历比较,而不用在所有的数据集中进行遍历。
为什么要用多表哈希?
对于单表哈希,当我们的哈希函数数目K取得太大,查询样本与其对应的最近邻落入同一个桶中的可能性会变得很微弱,针对这个问题,我们可以重复这个过程L次,从而增加最近邻的召回率。这个重复L次的过程,可以转化为构建L个哈希表,这样在给定查询样本时,我们可以找到L个哈希桶(每个表找到一个哈希桶),然后我们在这L个哈希表中进行遍历。这个过程相当于构建了K*L个哈希函数(注意是“相当”,不要做“等价”理解)。
多表哈希中哈希函数数目K和哈希表数目L如何选取?
哈希函数数目K如果设置得过小,会导致每一个哈希桶中容纳了太多的数据点,从而增加了查询响应的时间;而当K设置得过大时,会使得落入每个哈希桶中的数据点变小,而为了增加召回率,我们需要增加L以便构建更多的哈希表,但是哈希表数目的增加会导致更多的内存消耗,并且也使得我们需要计算更多的哈希函数,同样会增加查询相应时间。这听起来非常的不妙,但是在K过大或过小之间仍然可以找到一个比较合理的折中位置。通过选取合理的K和L,我们可以获得比线性扫描极大的性能提升。
Multiprobe LSH是为了解决什么问题?
多probe LSH主要是为了提高查找准确率而引入的一种策略。首先解释一下什么是Multiprobe。对于构建的L个哈希表,我们在每一个哈希表中找到查询样本落入的哈希桶,然后再在这个哈希桶中做遍历,而Multiprobe指的是我们不止在查询样本所在的哈希桶中遍历,还会找到其他的一些哈希桶,然后这些找到的T个哈希桶中进行遍历。这些其他哈希桶的选取准则是:跟查询样本所在的哈希桶邻近的哈希桶,“邻近”指的是汉明距离度量下的邻近。
通常,如果不使用Multiprobe,我们需要的哈希表数目L在100到1000之间,在处理大数据集的时候,其空间的消耗会非常的高,幸运地是,因为有了上面的Multiprobe的策略,LSH在任意一个哈希表中查找到最近邻的概率变得更高,从而使得我们能到减少哈希表的构建数目。
综上,对于LSH,涉及到的主要的参数有三个:
- K,每一个哈希表的哈希函数(空间划分)数目
- L,哈希表(每一个哈希表有K个哈希函数)的数目
- T,近邻哈希桶的数目,即the number of probes
这三个设置参数可以按照如下顺序进行:首先,根据可使用的内存大小选取L,然后在K和T之间做出折中:哈希函数数目K越大,相应地,近邻哈希桶的数目的数目T也应该设置得比较大,反之K越小,L也可以相应的减小。获取K和L最优值的方式可以按照如下方式进行:对于每个固定的K,如果在查询样本集上获得了我们想要的精度,则此时T的值即为合理的值。在对T进行调餐的时候,我们不需要重新构建哈希表,甚至我们还可以采用二分搜索的方式来加快T参数的选取过程。
LSH开源工具包
关于LSH开源工具库,有很多,这里推荐两个LSH开源工具包:LSHash和FALCONN, 分别对应于学习和应用场景。
LSHash
LSHash非常适合用来学习,里面实现的是最经典的LSH方法,并且还是单表哈希。哈希函数的系数采用随机的方式生成,具体代码如下:
def _generate_uniform_planes(self):
""" Generate uniformly distributed hyperplanes and return it as a 2D
numpy array.
"""
return np.random.randn(self.hash_size, self.input_dim)
hash_size为哈希函数的数目,即前面介绍的K。整个框架,不论是LSH的哈希函数的生成方式,还是LSH做查询,都极其的中规中矩,所以用来作为了解LSH的过程,再适合不过。如果要在实用中使用LSH,可以使用FALCONN。
FALCONN
FALCONN是经过了极致优化的LSH,其对应的论文为NIPS 2015 Practical and Optimal LSH for Angular Distance,Piotr Indyk系作者之一(Piotr Indyk不知道是谁?E2LSH这个页面对于看过LSH的应该非常眼熟吧),论文有些晦涩难懂,不过FALCONN工具包却是极其容易使用的,提供有C++使用的例子random_benchmark.cc以及Python的例子random_benchmark.py,另外文档非常的详实,具体可参阅falconn Namespace Reference和falconn module。下面将其Python例子和C++例子中初始化索引以及构建哈希表的部分提取出来,对其中的参数做一下简要的分析。
Python初始化与构建索引L127:
# Hyperplane hashing
params_hp = falconn.LSHConstructionParameters()
params_hp.dimension = d
params_hp.lsh_family = 'hyperplane'
params_hp.distance_function = 'negative_inner_product'
params_hp.storage_hash_table = 'flat_hash_table'
params_hp.k = 19
params_hp.l = 10
params_hp.num_setup_threads = 0
params_hp.seed = seed ^ 833840234
print('Hyperplane hash\n')
start = timeit.default_timer()
hp_table = falconn.LSHIndex(params_hp)
hp_table.setup(data)
hp_table.set_num_probes(2464)
C++初始化与构建索引L194:
// Hyperplane hashing
LSHConstructionParameters params_hp;
params_hp.dimension = d;
params_hp.lsh_family = LSHFamily::Hyperplane;
params_hp.distance_function = distance_function;
params_hp.storage_hash_table = storage_hash_table;
params_hp.k = 19;
params_hp.l = num_tables;
params_hp.num_setup_threads = num_setup_threads;
params_hp.seed = seed ^ 833840234;
cout << "Hyperplane hash" << endl << endl;
Timer hp_construction;
unique_ptr<LSHNearestNeighborTable<Vec>> hptable(
std::move(construct_table<Vec>(data, params_hp)));
hptable->set_num_probes(2464);
可以看到,有3个很重要的参数,分别是k、l和set_num_probes,对应的具体意义前面已经解释,这里不再赘述。
FALCONN的索引构建过程非常快,百万量级的数据,维度如果是128维,其构建索引时间大概2-3min的样子,实时搜索可以做到几毫秒的响应时间。总之,这是小白菜见过的构建索引时间最短查询响应时间也极快的ANN工具库。
另外谈一下数据规模问题。对于小数据集和中型规模的数据集(几个million-几十个million), FALCONN和NMSLIB是一个非常不错的选择,如果对于大型规模数据集(几百个million以上),基于矢量量化的Faiss是一个明智的选择。关于这方面的讨论,可以参阅小白菜参阅的讨论benchmark。
当然,FALCONN还不是很完善,比如对于数据的动态增删目前还不支持,具体的讨论可以参见Add a dynamic LSH table。其实这不是FALCONN独有的问题,NMSLIB目前也不支持。一般而言,动态的增删在实际应用场合是一个基本的要求,但是我们应注意到,增删并不是毫无限制的,在增删频繁且持续了一段时间后,这是的数据分布已经不是我们原来建索引的数据分布形式了,我们应该重新构建索引。在这一点上,Faiss支持数据的动态增删。
对于哈希方法及其典型代表局部敏感哈希,暂时就整理到这里了。下面小白菜对基于矢量量化的方法谈一谈自己理解。
矢量量化方法
矢量量化方法,即vector quantization,其具体定义为:将一个向量空间中的点用其中的一个有限子集来进行编码的过程。在矢量量化编码中,关键是码本的建立和码字搜索算法。比如常见的聚类算法,就是一种矢量量化方法。而在ANN近似最近邻搜索中,向量量化方法又以乘积量化(PQ, Product Quantization)最为典型。在之前的博文基于内容的图像检索技术的最后,对PQ乘积量化的方法做过简单的概要。在这一小节里,小白菜结合自己阅读的论文和代码对PQ乘积量化、倒排乘积量化(IVFPQ)做一种更加直观的解释。
PQ乘积量化
PQ乘积量化的核心思想还是聚类,或者说具体应用到ANN近似最近邻搜索上,K-Means是PQ乘积量化子空间数目为1的特例。PQ乘积量化生成码本和量化的过程可以用如下图示来说明:
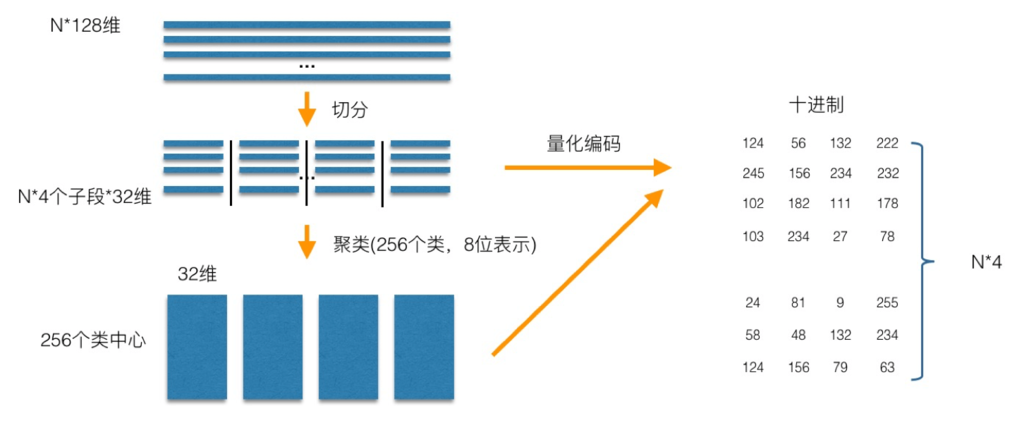
在训练阶段,针对N个训练样本,假设样本维度为128维,我们将其切分为4个子空间,则每一个子空间的维度为32维,然后我们在每一个子空间中,对子向量采用K-Means对其进行聚类(图中示意聚成256类),这样每一个子空间都能得到一个码本。这样训练样本的每个子段,都可以用子空间的聚类中心来近似,对应的编码即为类中心的ID。如图所示,通过这样一种编码方式,训练样本仅使用的很短的一个编码得以表示,从而达到量化的目的。对于待编码的样本,将它进行相同的切分,然后在各个子空间里逐一找到距离它们最近的类中心,然后用类中心的id来表示它们,即完成了待编码样本的编码。
正如前面所说的,在矢量量化编码中,关键是码本的建立和码字的搜索算法,在上面,我们得到了建立的码本以及量化编码的方式。剩下的重点就是查询样本与dataset中的样本距离如何计算的问题了。
在查询阶段,PQ同样在计算查询样本与dataset中各个样本的距离,只不过这种距离的计算转化为间接近似的方法而获得。PQ乘积量化方法在计算距离的时候,有两种距离计算方式,一种是对称距离,另外一种是非对称距离。非对称距离的损失小(也就是更接近真实距离),实际中也经常采用这种距离计算方式。下面过程示意的是查询样本来到时,以非对称距离的方式(红框标识出来的部分)计算到dataset样本间的计算示意:
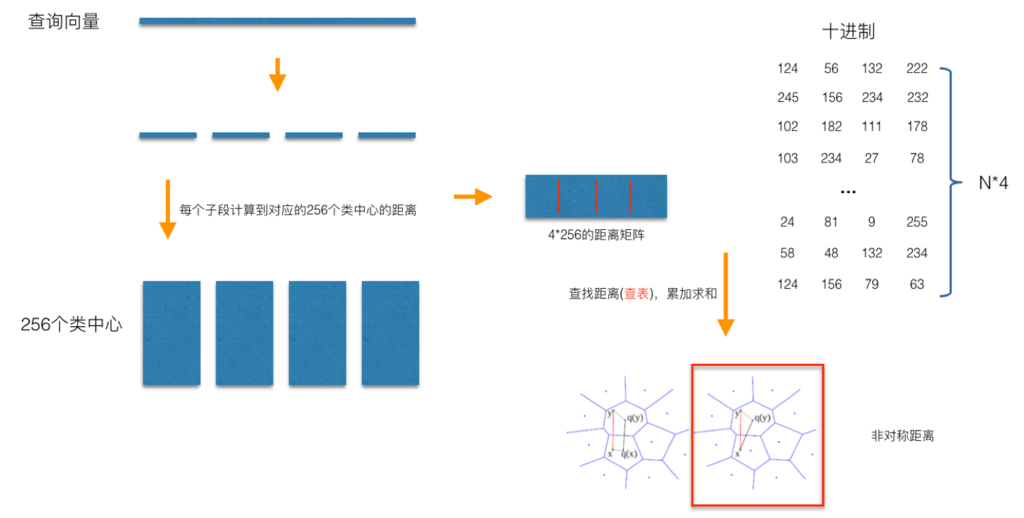
具体地,查询向量来到时,按训练样本生成码本的过程,将其同样分成相同的子段,然后在每个子空间中,计算子段到该子空间中所有聚类中心得距离,如图中所示,可以得到4*256个距离,这里为便于后面的理解说明,小白菜就把这些算好的距离称作距离池。在计算库中某个样本到查询向量的距离时,比如编码为(124, 56, 132, 222)这个样本到查询向量的距离时,我们分别到距离池中取各个子段对应的距离即可,比如编码为124这个子段,在第1个算出的256个距离里面把编号为124的那个距离取出来就可,所有子段对应的距离取出来后,将这些子段的距离求和相加,即得到该样本到查询样本间的非对称距离。所有距离算好后,排序后即得到我们最终想要的结果。
从上面这个过程可以很清楚地看出PQ乘积量化能够加速索引的原理:即将全样本的距离计算,转化为到子空间类中心的距离计算。比如上面所举的例子,原本brute-force search的方式计算距离的次数随样本数目N成线性增长,但是经过PQ编码后,对于耗时的距离计算,只要计算4*256次,几乎可以忽略此时间的消耗。另外,从上图也可以看出,对特征进行编码后,可以用一个相对比较短的编码来表示样本,自然对于内存的消耗要大大小于brute-force search的方式。
在某些特殊的场合,我们总是希望获得精确的距离,而不是近似的距离,并且我们总是喜欢获取向量间的余弦相似度(余弦相似度距离范围在[-1,1]之间,便于设置固定的阈值),针对这种场景,可以针对PQ乘积量化得到的前top@K做一个brute-force search的排序。
倒排乘积量化
倒排PQ乘积量化(IVFPQ)是PQ乘积量化的更进一步加速版。其加速的本质逃不开小白菜在最前面强调的是加速原理:brute-force搜索的方式是在全空间进行搜索,为了加快查找的速度,几乎所有的ANN方法都是通过对全空间分割,将其分割成很多小的子空间,在搜索的时候,通过某种方式,快速锁定在某一(几)子空间,然后在该(几个)子空间里做遍历。在上一小节可以看出,PQ乘积量化计算距离的时候,距离虽然已经预先算好了,但是对于每个样本到查询样本的距离,还是得老老实实挨个去求和相加计算距离。但是,实际上我们感兴趣的是那些跟查询样本相近的样本(小白菜称这样的区域为感兴趣区域),也就是说老老实实挨个相加其实做了很多的无用功,如果能够通过某种手段快速将全局遍历锁定为感兴趣区域,则可以舍去不必要的全局计算以及排序。倒排PQ乘积量化的”倒排“,正是这样一种思想的体现,在具体实施手段上,采用的是通过聚类的方式实现感兴趣区域的快速定位,在倒排PQ乘积量化中,聚类可以说应用得淋漓尽致。
倒排PQ乘积量化整个过程如下图所示:
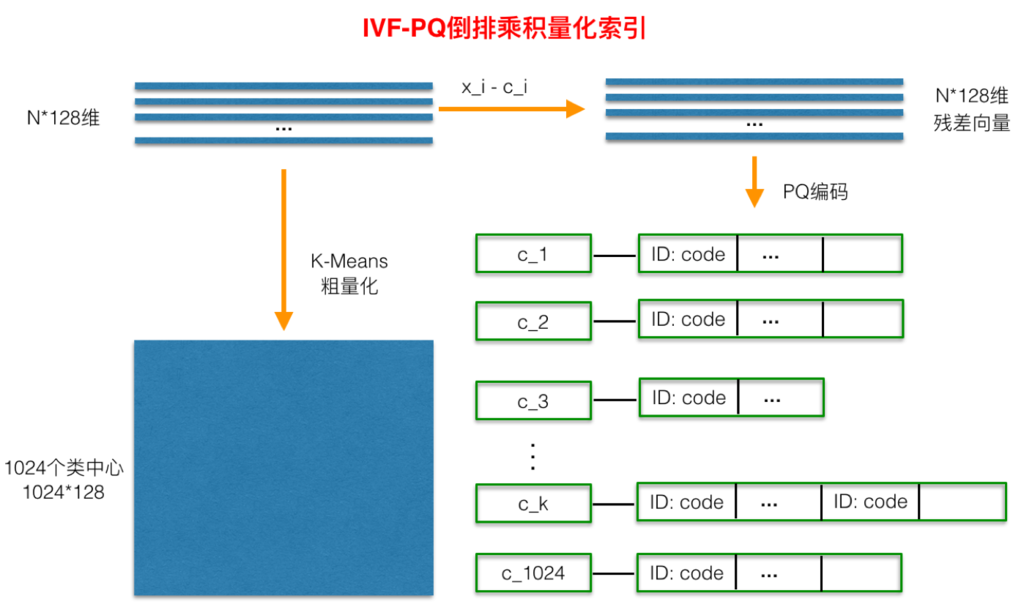
在PQ乘积量化之前,增加了一个粗量化过程。具体地,先对N个训练样本采用K-Means进行聚类,这里聚类的数目一般设置得不应过大,一般设置为1024差不多,这种可以以比较快的速度完成聚类过程。得到了聚类中心后,针对每一个样本x_i,找到其距离最近的类中心c_i后,两者相减得到样本x_i的残差向量(x_i-c_i),后面剩下的过程,就是针对(x_i-c_i)的PQ乘积量化过程,此过程不再赘述。
在查询的时候,通过相同的粗量化,可以快速定位到查询向量属于哪个c_i(即在哪一个感兴趣区域),然后在该感兴趣区域按上面所述的PQ乘积量化距离计算方式计算距离。
